Part 6: Path planning

Lastly, time to create the final path. A good path planner will do this task.

For these examples, we will continue from the previous tutorial:

C++
Python

f2c::Random rand(42);
F2CRobot robot (2.0, 6.0);
f2c::hg::ConstHL const_hl;
F2CCells cells = rand.generateRandField(1e4, 5).getField();
F2CCells no_hl = const_hl.generateHeadlands(cells, 3.0 * robot.getWidth());
f2c::sg::BruteForce bf;
F2CSwaths swaths = bf.generateSwaths(M_PI, robot.getCovWidth(), no_hl.getGeometry(0));
f2c::rp::SnakeOrder snake_sorter;
swaths = snake_sorter.genSortedSwaths(swaths);

rand = f2c.Random(42)
robot = f2c.Robot(2.0, 6.0)
const_hl = f2c.HG_Const_gen()
field = rand.generateRandField(1e4, 5)
cells = field.getField()
no_hl = const_hl.generateHeadlands(cells, 3.0 * robot.getWidth())
bf = f2c.SG_BruteForce()
swaths = bf.generateSwaths(math.pi, robot.getCovWidth(), no_hl.getGeometry(0))
snake_sorter = f2c.RP_Snake()
swaths = snake_sorter.genSortedSwaths(swaths)

Before continue, we will define the path planner and some parameters that will be needed for computing the turns:

C++
Python

robot.setMinTurningRadius(2);  // m
robot.setMaxDiffCurv(0.1);  // 1/m^2
f2c::pp::PathPlanning path_planner;

robot.setMinTurningRadius(2)  # m
robot.setMaxDiffCurv(0.1);  # 1/m^2
path_planner = f2c.PP_PathPlanning()

Any of these planners accept also a route input instead of a swaths.

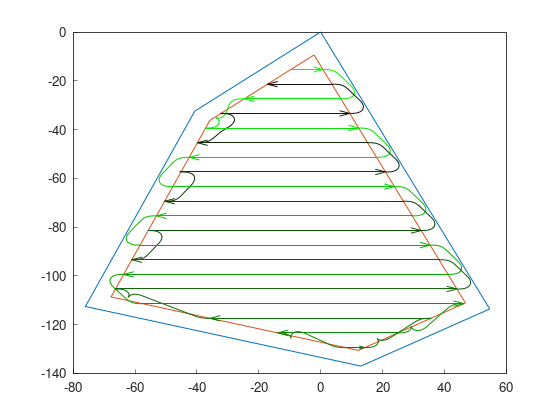
Dubins curves

Dubins curves are generated with 3 segments of turn. Segments of turn in Dubins are always going forward. Segment types are straight, right curve or left curve.

Dubins produces the shortest turn possible.

C++
Python

f2c::pp::DubinsCurves dubins;
F2CPath path_dubins = path_planner.planPath(robot, swaths, dubins);

dubins = f2c.PP_DubinsCurves()
path_dubins = path_planner.planPath(robot, swaths, dubins);

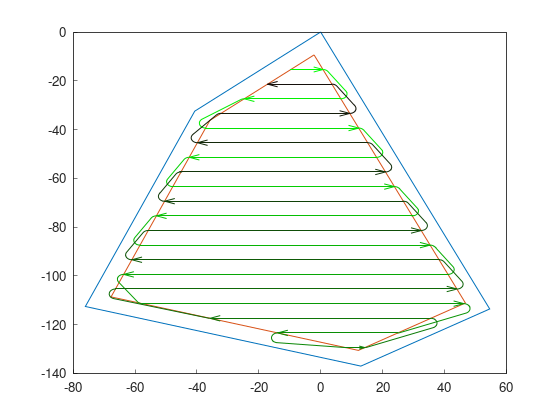
Dubins curves with Continuous curvature

While Dubins curves produces the shortest path possible, going from one segment of the curve to another creates instant curvature change. A vehicle could not follow a path with this issue, so this path planner implements an integrator to change the curvature smoothly.

C++
Python

f2c::pp::DubinsCurvesCC dubins_cc;
F2CPath path_dubins_cc = path_planner.planPath(robot, swaths, dubins_cc);

dubins_cc = f2c.PP_DubinsCurvesCC();
path_dubins_cc = path_planner.planPath(robot, swaths, dubins_cc);

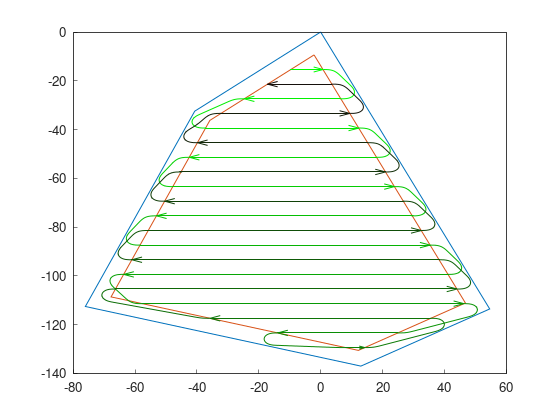
../../_images/Tutorial_6_2_Dubins_CC.png

Reeds-Shepp curves

Reeds-Shepp curves also computes the shortest path, but allowing the vehicle to go backwards.

C++
Python

f2c::pp::ReedsSheppCurves reeds_shepp;
F2CPath path_reeds_shepp = path_planner.planPath(robot, swaths, reeds_shepp);

reeds_shepp = f2c.PP_ReedsSheppCurves();
path_reeds_shepp = path_planner.planPath(robot, swaths, reeds_shepp);

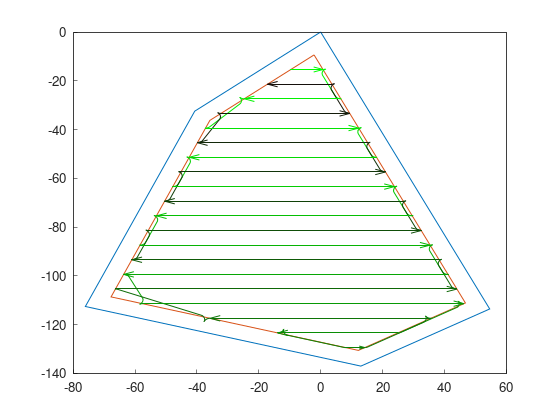
../../_images/Tutorial_6_3_Reeds_Shepp.png

Reeds-Shepp curves with Continuous curvature

As with Dubins, instantaneous curvature change is a problem in this kind of curves. This planner has an integrator to smooth the path.

C++
Python

f2c::pp::ReedsSheppCurvesHC reeds_shepp_hc;
F2CPath path_reeds_shepp_hc = path_planner.planPath(robot, swaths, reeds_shepp_hc);

reeds_shepp_hc = f2c.PP_ReedsSheppCurvesHC();
path_reeds_shepp_hc = path_planner.planPath(robot, swaths, reeds_shepp_hc);